이번 장의 주제는 합성곱 신경망(Convolutional Neural Network, CNN) 입니다. 내용적으로 반드시 따라나와야 하는 내용은 아니지만, 워낙 효과적이고 많이 쓰이기 때문에 딥러닝을 배울때 반드시 짚고 가는 내용입니다. 합성곱 신경망을 이해하기 위해서는 합성곱 계층과 풀링 계층을 알아야 합니다.
0. 채널 (Channel)
하지만 우선 layer들을 살펴보기 전에 channel이 무슨 개념인지 알고 갑시다.

만약 컴퓨터에서 어떤 이미지를 RGB로 처리한다고 하면, 다음과 같이 이미지를 R, G, B 세개 channel의 결합으로 생각할 수 있습니다. 이와 비슷하게 뒤에 볼 Convolutional Layer를 거치면 같은 이미지에 대한 Feature Map(2차원 배열입니다)이 커널의 개수만큼 생기게 되는데, 각 Feature Map을 하나의 channel로 생각하면 이를 여러 channel을 가진 하나의 Feature Map으로 생각할 수 있습니다. 그냥 Feature Map들을 길게 늘이지 않고 channel로 나누는 이유는 local connectivity를 이용하기 위해서입니다. 이미지를 처음부터 하나의 긴 벡터가 아니라 2차원의 이미지로 처리하는 것과 같은 맥락입니다.

이를 3차원 배열로 생각한다면 width x height x (channel의 개수) 의 배열로 생각할 수 있습니다. 그렇기 때문에 channel의 개수를 depth 라고 표현합니다.
1. 합성곱 계층 ( Convolution Layer )
합성곱 계층에서는 필터(커널)을 이용한 합성곱 연산을 진행합니다.
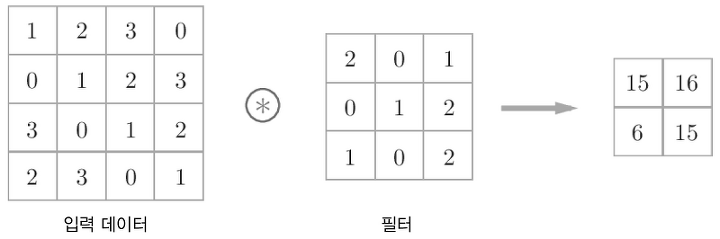
위 그림처럼 2차원의 입력 데이터에 대해서 주어진 필터를 이동시키며 입력 데이터의 각 3 x 3 지역마다 필터에서 대응하는 원소끼리 곱한 후 이를 모두 합해줍니다. 이때 각 입력 데이터의 각 3 x 3 지역을 window라고 하며, 각 window에 대해서 이를 모두 수행해서 출력 배열의 해당 위치에 값을 적어주면 됩니다. 이때 필터의 각 값을 Fully Connected Layer에서의 가중치라고 생각할 수 있습니다. 따라서 이는 앞의 fully connected layer 에서 특정 위치를 제외한 다른 모든 가중치를 0으로 만드는 것으로 볼 수도 있습니다.

fully connected layer들과 마찬가지로 convolution layer에도 편향을 적용할 수 있습니다. 위 그림처럼 별 다를것 없이 그냥 더해주면 되지만, 2 x 2 배열로 편향이 있는것이 아니라 배열 전체에 같은 값을 더해주는것입니다.

이제 앞에서 본 channel을 적용시켜 봅시다. 위 그림처럼 입력 데이터의 channel 개수가 3개라면, 즉 depth가 3이라면, 필터의 channel개수도 3개여야 합니다. 이 필터 자체는 channel마다 서로 다르지만, 필터의 크기는 모두 같아야 합니다. 사실 다차원 배열로 이해하면 좀 더 간단합니다. 4 x 4 x 3 의 입력 데이터에 3 x 3 x 3의 필터를 적용하는 것입니다. 필터 n개를 적용하면 출력 데이터는 2 x 2 x n의 배열이 되겠죠. 아주 간단하죠?
1. 1 합성곱 계층의 Hyperparameters
- Padding
padding은 출력 데이터 배열의 크기를 조정하기 위해서 이미지의 주변을 채워주는 것을 말합니다. 다른 종류의 padding도 있지만 가장 일반적인것은 그냥 0으로 채워주는 zero-padding입니다.

same padding은 padding을 통해서 이미지의 크기를 똑같이 유지해주는 padding을 말하며, valid padding이란 실제 값만 사용하는 것, 즉 padding을 하지 않는 것을 뜻합니다.
- Stride

stride는 kernel을 적용하는 간격을 뜻합니다. 지금까지 예시로 본 그림들은 모두 stride가 1인 경우였지만, 이는 . 당연하게도 stride가 커질수록 출력 배열의 크기는 줄어듭니다.
입력크기를 H x W, 필터 크기를 FH x FW, 출력크기를 OH x OW 패딩 크기를 P, 스트라이드를 S라고 하면 출력 크기는 다음과 같이 계산됩니다. 조금만 생각해보면 굉장히 당연한 식입니다.

그러면 출력의 Depth는?
- Depth
출력 데이터 배열의 depth는 몇번 나왔듯이 kernel의 개수입니다.
2. 풀링 계층 (Pooling Layer)

pooling은 데이터의 크기를 줄이는 downsampling의 일종입니다. 위 그림은 2 x 2 max pooling 으로, 앞에 Convolution Layer처럼 각 2 x 2 지역마다 값들 중 최대값을 선택해주면 됩니다. pooling에서 stride의 크기는 보통 window의 크기와 같게 설정합니다. 즉 겹치는 부분 없이 이미지를 한번만 훑겠다는 것이죠. pooling은 channel마다 독립적으로 계산하기 때문에 channel의 개수, 즉 depth는 그대로 유지됩니다.
pooling layer는 convolution layer와 다르게 학습을 하는 layer가 아닙니다. pooling의 종류 (max, average ...)와 window의 크기만 설정하면 더이상 학습할 것이 없기 때문입니다. 따라서 신경망적인 layer라기 보다는 그냥 downsampling하는 처리과정이라고 생각하셔도 됩니다.
3. CNN이 갖는 이점
우선 최종적으로 만들어지는 Convolutional Neural Network 의 구조는 다음과 같습니다. 마지막에는 Fully Connected Layer가 적어도 하나는 필요합니다. 어찌됬건 답으로는 0,1,2,...9를 알려주는 길이 10짜리 벡터를 출력해야 하니까요.

마지막의 Flattend 는 3차원 배열로 되어있는 이미지를 1차원의 긴 벡터로 만드는것을 뜻합니다. 앞에서 봤던 Fully Connected Neural Network 에서는 맨 처음에 해줄 작업이죠. 여기에서 우리는 CNN이 앞에서 봤던 그냥 신경망에 비해서 갖는 이점을 알 수 있습니다. 그냥 신경망에서는 이미지를 이미지로 보지 않고 처음부터 하나의 긴 벡터로 생각합니다. 하지만 보통 이미지에서는 2차원 배열로 봤을때 비슷한 위치에 있는 픽셀들이 모여서 하나의 feature를 나타내는데, 그냥 Neural Network에서는 이를 캐치하는 능력이 너무 떨어진다는 것이죠. CNN은 각 단계에서의 데이터를 하나의 긴 벡터가 아니라 다차원 배열, 즉 channel이 여러개인 이미지로 봄으로써 이 feature들을 효과적으로 추출해낸다는 것입니다. 이렇게 각 위치의 feature를 보는 것은 실제로 사람이 이미지를 처리하는 방법으로도 알려져 있습니다. 그리고 가장 중요한 것은 이유가 어찌됬건 CNN이 실제로 엄청나게 좋은 성능을 보인다는 것입니다.
'Machine Learning' 카테고리의 다른 글
| [CS231n] 9. CNN Architecture (0) | 2020.01.15 |
|---|---|
| [CS231n] 10. Recurrent Neural Networks (0) | 2020.01.11 |
| [Deep Learning from Scratch] 8. 딥러닝 (0) | 2020.01.09 |
| [Deep Learning from Scratch] 6장. 학습 관련 기술들 (0) | 2020.01.08 |
| [Deep Learning from Scratch] 5장. 오차역전파 (0) | 2020.01.08 |



