머신러닝에는 3종류의 방법이 있습니다.
- Supervised Learning
- Unsupervised Learning
- Reinforcement Learning
지도학습(Supervised Learning)은 인풋데이터와 아웃풋데이터가 정해져 있고 이를 토대로 학습하여 인풋데이터에 맞는 아웃풋이 나올 수 있도록 학습합니다. 비지도학습(Unsupervised Learning)은 인풋데이터에 대한 결과가 정해져있지 않을 때의 학습 방법입니다. 보통 특성이 많은 데이터를 간단하게 줄여서 나타내거나 비슷한 데이터들끼리 묶는 클러스터링 등의 방법을 사용합니다. 강화학습(Reinforcement Learning)은 주어진 상황에서 보상을 최대화할 수 있도록 하는 행동을 학습하는 방법을 의미합니다. 이번 포스트에서는 머신러닝에서 제일 중요하고 많이 사용하는 지도학습에서 쓰는 모델들에 대해서 간단한 원리와 사용방법에 대해서 알아보도록 하겠습니다.
다음은 지도학습에서 쓰는 모델들입니다.
- Linear Regression
- Logistic Regression
- Decision Tree
- SVM(Support Vector Machine)
- Navie Bayes
- KNN
Linear Regression
Definition
선형 회귀는 한개나 복수개의 x와 종속변수 y의 선형 상관관계를 알아내는 회귀 방법입니다.

위 그림은 한 개의 x에 대한 선형 회귀 예시입니다. 우리의 목표는 이 빨간 직선을 찾는 것입니다.
Principle
이 직선은 다음 식으로 나타낼 수 있습니다. 만약 x가 여러개라면 W, x 행렬로 생각하면 됩니다.
$$ y = W*x + b $$
W는 가중치(Weight), b는 편향(bias)라고 부릅니다.
그렇다면 이 직선을 찾기 위해서 W, b를 찾아야 하는데 어떻게 할 수 있을까요?
일반적으로 이 식에 모든 값이 정확하게 맞을 수는 없습니다. 그렇기에 데이터들에 제일 일치하는 직선이 어떤 직선인지를 정의합니다.
$$ Cost(W,b) = \frac{1}{m}\sum_{i=1}^{m}
(H(x^{(i)}) - y^{(i)})^2 $$
\(H(x) = W * x + b\)(W, b는 추정값입니다.)
목표는 이 cost 함숫값을 최소화하는 W, b를 찾는 것입니다.
최소화하기 위한 방법으로 Gradient Descent Algorithm을 사용합니다.
$$ W \Leftarrow W - \alpha {\sigma \over \sigma W} cost(W,b) $$
$$ b \Leftarrow b - \alpha {\sigma \over \sigma W} cost(W,b) $$
\( \alpha\) : learning rate
적절한 learning rate를 정하면 위 수식처럼 W, b를 매번 변경시켜주면서 여러 단계 학습을 거치면 cost를 최소화하는 W, b를 찾을 수 있습니다. W, b를 찾고나면 임의의 인풋에 대해서 꽤 정확한 아웃풋을 찾아줄 수 있을 것입니다.
Target
- Regression
- feature : multi, continuous
- label : continuous
회귀에서만 사용가능합니다. 연속적인 값을 갖고있는 피처 복수개에 대해 사용가능하며 라벨은 연속적인 값으로 나타나집니다.
Example code
>>> import numpy as np
>>> from sklearn.linear_model import LinearRegression
>>> X = np.array([[1, 1], [1, 2], [2, 2], [2, 3]])
>>> # y = 1 * x_0 + 2 * x_1 + 3
>>> y = np.dot(X, np.array([1, 2])) + 3
>>> reg = LinearRegression().fit(X, y)
>>> reg.score(X, y)
1.0
>>> reg.coef_
array([1., 2.])
>>> reg.intercept_
3.0000...
>>> reg.predict(np.array([[3, 5]]))
array([16.])Logistic Regression
Definition
Logistic Regression는 아우풋으로 0과 1만 나오는 회귀 방법입니다. 이런 경우에는 선형회귀로 하기에는 굉장히 어려움이 많습니다.
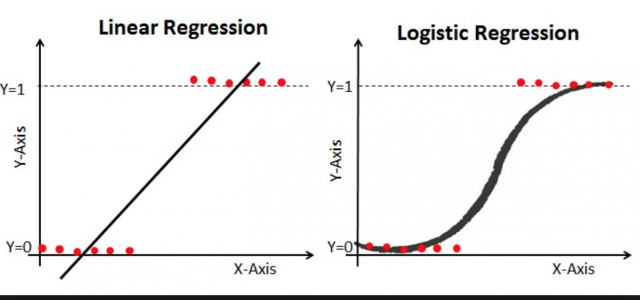
이 그림은 Linear Regression과 Logistic Regression의 차이를 보여줍니다.
로지스틱 회귀에서의 목표는 이 곡선을 찾는 것입니다.
Principle
- Linear Regression : \( Y = W*x+b \)
- Logistic Regression : \( ln({1-p \over p}) = W *x +b \Rightarrow p = {1 \over {1+e^{W*x+b}}} \)
p가 1/2 이상이면 1, 1/2 이하면 0이 됩니다.
이 곡선은 다음과 같은 시그모이드 함수를 사용하여 나타냅니다.
\(sigmoid(x) = {1 \over 1+e^x}\)
$$ H(x) = sigmoid(W*x+b) $$
로지스틱 회귀에서 cost 함수는 이렇게 나타낼 수 있습니다.
$$ Cost(H(x), y) = -ylog(H(x))+(1-y)log(1-H(x)) $$
y가 1일 때에는 \( Cost(H(x), y) = -log(H(x)) \)이 되고 \(H(x)\)가 1로 접근할 때 cost가 감소합니다. y가 0이면 \( Cost(H(x), y) = log(1-H(x)) \) 이 되고 \(H(x)\)가 0으로 접근할 때 cost가 감소합니다.
즉, 우리가 이 함숫값을 최소화시킨다면 최선의 H(x)를 찾을 수 있습니다. 그렇다면 이 함숫값은 어떻게 최소화시킬까요?
위와 마찬가지로 gradient descent algorithms를 사용합니다.
자세한 원리는 선형 회귀의 경우와 같기 때문에 생략합니다. 미분한 수식만이 달라지게 됩니다.
Target
- Classification
- feature : multi, continuous
- label : binary
0과 1로 분류를 할 때 사용합니다. 연속적인 값을 가지는 여러개의 피처에 대해 0과 1로만 결과가 나오게 됩니다.
Example code
>>> from sklearn.datasets import load_iris
>>> from sklearn.linear_model import LogisticRegression
>>> X, y = load_iris(return_X_y=True)
>>> clf = LogisticRegression(random_state=0, solver='lbfgs',
... multi_class='multinomial').fit(X, y)
>>> clf.predict(X[:2, :])
array([0, 0])
>>> clf.predict_proba(X[:2, :])
array([[9.8...e-01, 1.8...e-02, 1.4...e-08],
[9.7...e-01, 2.8...e-02, ...e-08]])
>>> clf.score(X, y)
0.97...Decision Tree
Definition
결정 트리는 분류와 회귀 모두 가능합니다.

이 그림은 결정 트리에 대해서 정확하게 설명하고 있습니다. 하나씩 질문을 하고 그 대답에 따라 하나씩 따라가 최종 결과에 다다르게 됩니다. 회귀의 경우에는 마지막 노드의 y값들의 평균으로 아웃풋을 구합니다.
Principle
결정 트리는 부모 노드에서 자식 노드로 갈 때 각 노드의 순도를 높이는 방향으로 학습됩니다. 일반적으로 순도를 계산할 때 많이 쓰는 엔트로피 계산 방법을 여기에서도 사용합니다. m개의 레코드가 속하는 area A의 엔트로피는 다음 식으로 정의됩니다.
$$ Entropy(A) = -\sum_{k=1}^m p_k \log_2 p_k $$
\( p_k \) : 영역A에서 카테고리 k의 레코드 백분율
만약 이 계산 결과가 부모 노드를 자식 노드 여러개로 나누기 전보다 작다면 나누고 그렇지 않다면 다른 기준을 찾거나 나누지 않습니다.
자세한 순서입니다.
- 데이터 정렬
- 1~i번째까지의 데이터 vs 나머지 데이터
- 엔트로피를 계산하고 기존 엔트로피와 비교
- 기존 엔트로피보다 작은 엔트로피가 나오는 i를 찾음
- 나눔
- 재귀적으로 반복
모든 과정이 종료가 되면 브랜치를 일부분 잘라냅니다. 너무 많은 브랜치를 만들어 과적합되었을 수도 있습니다.
Target
- Classification, Regression
- feature : multi, categorical, continuous
- label : categorical, continuous
분류, 회귀 모두 가능하며 분류일 때에는 categorical data, 회귀일 때는 continuous data를 사용합니다.
Example code
from sklearn import tree from sklearn.datasets import load_iris import graphviz
X = [[0, 0], [1, 1]]
Y = [0, 1]
clf = tree.DecisionTreeClassifier()
clf = clf.fit(X, Y)
print(clf.predict([[2.,2.]]))
iris = load_iris()
clf = tree.DecisionTreeClassifier()
clf = clf.fit(iris.data, iris.target)
dot_data = tree.export_graphviz(clf, out_file=None,
feature_names=iris.feature_names,
class_names=iris.target_names,
filled=True, rounded=True,
special_characters=True)
graph = graphviz.Source(dot_data)
graph
[1]
SVM(Support Vector Machine)
Definition
서포트 벡터 머신 알고리즘은 데이터 포인트들을 나누는 직선(초평면)을 찾는 알고리즘입니다. 정확히는 maximum margin(여러개로 분류되어있는 데이터 점들 중에서 선과 제일 가까운 점의 최대 거리)를 갖게 하는 직선(초평면)을 찾는 것입니다. 회귀의 경우에는 직선까지의 거리가 엡실론(하이퍼파라미터)보다 작은 점들이 최대화되도록 하는 직선(초평면)을 찾습니다. 인풋 데이터가 2개인 경우에는 직선, 그 이상이면 초평면이 됩니다.
Principle
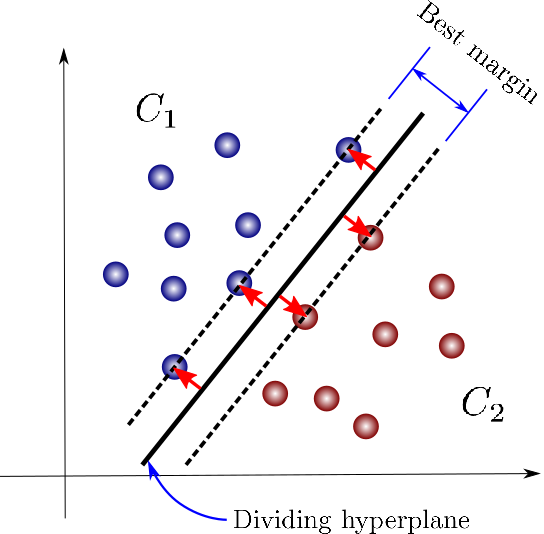
SVM는 제일 큰 마진을 만드는 직선(초평면)을 찾습니다.
Hinge loss는 maximum-margin classification에서 사용합니다. 이 loss를 최소화하면 margin이 최대화됩니다.
$$f(x) = W*x+b $$
$$Cost(x,y,f(x)) = max(0, 1-y*f(x))$$
예측 값과 실제 값이 같은 부호면 cost는 0이 됩니다. 이번에도 gradient descent algorithm을 사용하여 가중치를 업데이트합니다.
SVM에는 linear SVM, rbf SVM 등등이 있습니다. 여기서는 제일 중요한 이 2개만을 설명하려고 합니다. Linear SVM은 SVM의 기본으로 직선으로 나눠 원이 경계일 경우 한계가 있지만 rbf SVM은 이런 경우에도 분류가 가능합니다.
Kernel 함수가 고차원으로 데이터들을 사상시켜주고 한 차원 위에서 분류를 하는 것입니다. 이런 경우에 Linear SVM은 분류할 수 없지만 rbf SVM은 가능합니다.
Target
- Classification, Regression
- feature : multi, continuous
- label : continuous
분류, 회귀 모두 가능하며 연속적인 값에 대해서만 사용할 수 있습니다.
Example
code>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [1, 1], [2, 1]])
>>> y = np.array([1, 1, 2, 2])
>>> from sklearn.svm import SVC
>>> clf = SVC(gamma='auto')
>>> clf.fit(X, y)
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
>>> print(clf.predict([[-0.8, -1]]))
[1]Naive Bayes
Definition
이 모델은 베이즈 정리로부터 파생되었습니다. 베이즈 정리는 다음과 같습니다.
$$P(c|x) = {P(x|c)P(c) \over P(x)}$$
\(P(c|x)\) : 사후 확률(Posterior Probability)
\(P(x|c)\) : 가능성(Likelihood)
\(P(c)\) : 클래스 사전 고유 확률(Class Prior Probability)
\(P(x)\) : 사전 확률(Predictor Prior probability)
Naive Bayes는 이 베이즈 정리를 기반으로 한 분류기입니다. Naive라는 형용사가 붙은 이유는 사용하기 위한 조건이 상당히 어려워서입니다. 바로 모든 피처들이 서로 확률적으로 독립되어야 한다는 점입니다. 이 경우에만 분류가 가능합니다.
Principle
모든 피처가 확률적으로 독립일 때 다음 수식으로 나타낼 수 있습니다.
$$P(c|X) = P(x_1|c) \times P(x_2|c) \times \cdots \times P(x_n|c) \times P(c)$$
X가 아무리 많은 피처를 갖고 있어도 걱정할 필요가 없습니다. 그냥 P(c|X)를 계산하면 됩니다. 제일 큰 확률을 가지는 라벨값이 아웃풋이 됩니다.
이 모델은 numeric data에 대해서도 적용가능하지만 categorical data에 훨씬 효율적입니다.
Target
- Classification
- feature : categorical, multi
- label : categorical
분류만 가능하고 이론적으로 numeric data여도 되긴 하지만 categorical data에 대해서만 사용하는 것을 추천합니다.
Example code
>>> import numpy as np
>>> X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
>>> Y = np.array([1, 1, 1, 2, 2, 2])
>>> from sklearn.naive_bayes import GaussianNB
>>> clf = GaussianNB()
>>> clf.fit(X, Y)
GaussianNB(priors=None, var_smoothing=1e-09)
>>> print(clf.predict([[-0.8, -1]]))
[1]
>>> clf_pf = GaussianNB()
>>> clf_pf.partial_fit(X, Y, np.unique(Y))
GaussianNB(priors=None, var_smoothing=1e-09)
>>> print(clf_pf.predict([[-0.8, -1]]))
[1]KNN
Definition
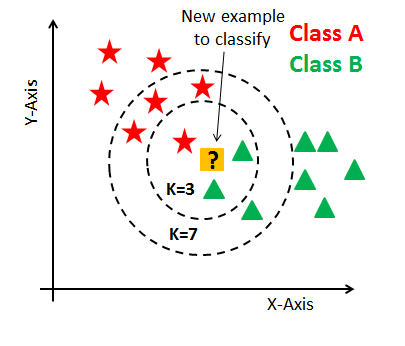
어떤 데이터에 대해 제일 가까운 데이터부터 확인하여 가장 많은 데이터를 포함하고 있는 그룹으로 분류합니다. k는 확인할 데이터의 갯수를 의미합니다.
회귀의 경우에는 k개의 데이터의 y값의 평균으로 계산됩니다.
Principle
만약 k가 3이면 B가 2개, A가 1개이므로 B로 분류됩니다. k가 7이면 A가 4개, B가 3개이므로 A로 분류됩니다.
그러면 거리는 어떻게 계산될까요?
Euclidean distance로 계산되는데 각 피처는 전부 다른 단위를 갖고 있는데 엄청 큰 단위를 갖고 있는 피처의 경우 값이 매우 작기에 무시될 가능성이 매우 큽니다. 이런 이유로 normalization이 꼭 필수적입니다. 마지막 문제는 최적의 k를 찾는 것인데 이는 Validation data를 잘 분류하는 k가 얼마인지 찾으면 됩니다.
Target
- Classification, Regression
- feature : continuous, categorical, multi
- label : continuous, categorical
분류, 회귀 모두 가능하며 데이터의 형식에도 상관없습니다.
Example code
>>> X = [[0], [1], [2], [3]]
>>> y = [0, 0, 1, 1]
>>> from sklearn.neighbors import KNeighborsClassifier
>>> neigh = KNeighborsClassifier(n_neighbors=3)
>>> neigh.fit(X, y)
KNeighborsClassifier(...)
>>> print(neigh.predict([[1.1]]))
[0]
>>> print(neigh.predict_proba([[0.9]]))
[[0.66666667 0.33333333]]'Machine Learning' 카테고리의 다른 글
| 컴퓨터의 시각 인식에 대해 알아보자 (0) | 2019.10.28 |
|---|---|
| Boosting과 친해져보자! (0) | 2019.10.27 |
| 중학생도 쉽게 이해하는 Gaussian Naive Bayes Classifier (2) | 2019.10.26 |
| Ensemble의 기법 (1) | 2019.10.23 |
| Epoch, Batch, Iteration 용어 정리 (0) | 2019.10.16 |




